Soal 1
Ketika sebuah satelit berada 106 m dari bulan, periode orbitnya adalah 25 menit. Ketika satelit tersebut turun ke orbit yang lebih rendah 1,6 x 105 m, periode barunya adalah ....
A. 36 s
B. 54 s
C. 72 s
D. 84s
E. 96 s
Jawab:
Hukum III Kepler menjelaskan hubungan antara periode dengan jari-jari orbit satelit yang dinyatakan sebagai
T2 = Cr3, dengan C suatu konstanta
Persamaan di atas dapat kita tuliskan sebagai
(T1/T2)2 = (R1/R2)3
(25 menit/T2)2 = (106/1,6 x 105)3
T2 = 1,6 menit = 96 s
Soal 2
Planet A dan B masing masing berjarak rata-rata sebesar p dan q terhadap matahari. Planet A mengitari Matahari dengan periode T. Jika p = 4q, planet B mengitari Matahari dengan periode sebesar . . . .
A. T/12
B. T/10
C. T/8
D. T/6
E. T/4
Jawab:
Hukum III Kepler menjelaskan hubungan antara periode dengan jari-jari orbit satelit yang dinyatakan sebagai
T2 = Cr3, dengan C suatu konstanta
Persamaan di atas dapat kita tuliskan sebagai
(TA/TB)2 = (RA/RB)3
(T/TB)2 = (4q/q)3
TB = T/8
Soal 3
Sebuah satelit mengorbit bumi yang memiliki jari-jari R. Grafik yang menampilkan kelajuan v dari satelit terhadap r, jarak satelit ke pusat bumi adalah . . . .
Jawab:
Sebuah satelit mengorbit Bumi pada jarak R dinyatakan sebagai
v = [GM/r]1/2
Grafik yang menampilkan kelajuan v dari satelit terhadap r, jarak satelit ke pusat bumi adalah
Soal 4
Pertimbangan kemungkinan suatu tembakan mengitari bumi. Sebuah benda dilembar secara horizontal pada radius r mengitari bumi yang dianggap berbentuk bola. Periode benda tersebut adalah . . . .
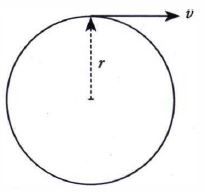
Jawab:
Ketika mengorbit Bumi, gaya tarik-menarik pada benda berperilaku sebagai gaya sentripetal (karena orbit berupa lingkaran), maka persamaan di atas kita tulis menjadi
mv2/r = GmM/r2
v = √(GM/r) (v semakin kecil jika r bertambah)
dengan v = kecepatan orbit (kecepatan linear singgung) benda.
Periode benda diberikan oleh
2πr/T = √(GM/r)
T = 2π√[r3/GM]
Ketika sebuah satelit berada 106 m dari bulan, periode orbitnya adalah 25 menit. Ketika satelit tersebut turun ke orbit yang lebih rendah 1,6 x 105 m, periode barunya adalah ....
A. 36 s
B. 54 s
C. 72 s
D. 84s
E. 96 s
Jawab:
Hukum III Kepler menjelaskan hubungan antara periode dengan jari-jari orbit satelit yang dinyatakan sebagai
T2 = Cr3, dengan C suatu konstanta
Persamaan di atas dapat kita tuliskan sebagai
(T1/T2)2 = (R1/R2)3
(25 menit/T2)2 = (106/1,6 x 105)3
T2 = 1,6 menit = 96 s
Soal 2
Planet A dan B masing masing berjarak rata-rata sebesar p dan q terhadap matahari. Planet A mengitari Matahari dengan periode T. Jika p = 4q, planet B mengitari Matahari dengan periode sebesar . . . .
A. T/12
B. T/10
C. T/8
D. T/6
E. T/4
Jawab:
Hukum III Kepler menjelaskan hubungan antara periode dengan jari-jari orbit satelit yang dinyatakan sebagai
T2 = Cr3, dengan C suatu konstanta
Persamaan di atas dapat kita tuliskan sebagai
(TA/TB)2 = (RA/RB)3
(T/TB)2 = (4q/q)3
TB = T/8
Soal 3
Sebuah satelit mengorbit bumi yang memiliki jari-jari R. Grafik yang menampilkan kelajuan v dari satelit terhadap r, jarak satelit ke pusat bumi adalah . . . .
Jawab:
Sebuah satelit mengorbit Bumi pada jarak R dinyatakan sebagai
v = [GM/r]1/2
Grafik yang menampilkan kelajuan v dari satelit terhadap r, jarak satelit ke pusat bumi adalah
Soal 4
Pertimbangan kemungkinan suatu tembakan mengitari bumi. Sebuah benda dilembar secara horizontal pada radius r mengitari bumi yang dianggap berbentuk bola. Periode benda tersebut adalah . . . .

Jawab:
Ketika mengorbit Bumi, gaya tarik-menarik pada benda berperilaku sebagai gaya sentripetal (karena orbit berupa lingkaran), maka persamaan di atas kita tulis menjadi
mv2/r = GmM/r2
v = √(GM/r) (v semakin kecil jika r bertambah)
dengan v = kecepatan orbit (kecepatan linear singgung) benda.
Periode benda diberikan oleh
2πr/T = √(GM/r)
T = 2π√[r3/GM]

Post a Comment for "Soal dan Pembahasan Hukum Newton tentang Gravitasi 3"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!