Soal dan Pembahasan Jembatan Wheatstone

Soal 1

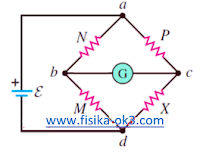
Jembatan Wheatstone pada gambar mempunyai data R_M = 12 Ω, R_X = 8 Ω, dan R_N = 3 Ω. Jika R_P diparalel dengan hambatan 3 Ω tercapai keseimbangan.

Hambatan R_p adalah . . . .

A. 6 Ω
B. 7 Ω
C. 8 Ω
D. 9 Ω
E. 10 Ω

Jawab:
Misalkan, nilai hambatan pengganti untuk hubungan paralel R_p dengan 3 Ω  adalah R. Sesuai dengan prinsip jembatan Wheatstone dalam keadaan setimbang berlaku
R_MR = R_NR_X
12 Ω x R = 8 Ω x 3 Ω
R = 2 Ω
R adalah gabungan R_P dengan 3 Ω secara paralel, sehingga
R = R_P(3 Ω)/(R_P + 3 Ω)
2(R_P + 3) = 3R_P
R_P = 6 Ω

Soal 2

Pada rangkaian di atas, tentukan: (a) nilai hambatan pengganti AB (R_AB)?, (b) besar kuat arus I? Dan (c) tegangan jepit rangkaian V_AB.

Jawab:

• Perkalian hambatan yang bersilang adalah sama (R₁R₄ = R₂R₃), sehingga rangkaian merupakan jembatan wheatstone dalam keadaan seimbang. Dengan demikian, R₅ tidak dilalui oleh arus, yang berarti dapat dihilangkan dari rangkaian. Rangkaian penggantinya seperti gambar di bawah ini.

Hambaran R₁ seri dengan R₃ menghasilkan hambatan penggati R_S1 = 4 Ω + 5 Ω = 9 Ω, sedangkan hambatan R₂ seri dengan R₄ menghasilkan hambatan pengganti R_S2 = 8 Ω + 10 Ω = 18 Ω.
Maka hambatan pengganti R_AB merupakan hubungan paralel R_S1 dengan R_S2, sehingga
R_AB = R_S1R_S2/(R_S1 + R_S2) = 9 Ω x 18 Ω/(9 Ω + 18 Ω) = 6 Ω

• Besar arus listrik adalah

I = ε/(R_AB + r) = 12 V/(6 Ω + 2 Ω) = 1,5 A

• Tegangan jepit rangkaian adalah

V_AB = IR_AB = (1,5 A)(6 Ω) = 9 V

Soal 3
Kesetimbangan rangkaian akan tercapai apabila hambatan x diseri dengan hambatan 9 Ω atau y diparalelkan dengan 12 Ω. Tentukan nilai X dan Y!

 

Jawab:
Dari soal ini rangkaian dapat kita gambarkan lagi seperti di bawah ini!

Jika rangkaian dalam keadaan setimbang, maka untuk rangkaian kiri berlaku:

2(x + 9) = 3y
2x = 3y – 18  (*)
Dan untuk rangkaian kanan berlaku:
2x = 3[12y/(12 + y)] (**)
Dari kedua persamaan di atas,
3[12y/(12 + y)] = 3y – 18
12y/(12 + y) = y – 6
(12 + y)(y – 6) = 12y
y² + 6y – 12(6) = 12y
y² – 6y – (12)(6) = 0
(y – 12)(y + 6) = 0
y = 12 Ω
maka dari (*) kita peroleh
2x = 3(12 Ω) – 18
x = 9 Ω

Soal 4
Gambar berikut adalah rangkaian jembatan Wheatstone, dengan panjang kawat homogen AB adalah 1 m. Ketika kontak geser C sedemikian sehingga jarak CB = 60 cm maka jembatan seimbang (Galvanometer G menunjuk nol). Jika ada X disisipkan seri resistor 10 Ω, maka jembatan seimbang ketika kontak C digeser sejauh 30 cm dari kedudukan seimbang semula. Tentukan nilai X dan Y!

 

Jawab:
AB = 1 m = 100 cm.
Pada kedudukan seimbang mula-mula, CB = 60 cm, AC = 100 cm – 60 cm = 40 cm.
Dari syarat jembatan seimbang kita peroleh
(X)(CB) = (Y)(AC)
(X)(60 cm) = Y(40 cm)
Y = 3X/2 (*)

Keadaan sekarang, pada X disisipkan resistor 10 Ω, sehingga hambatan total = (X + 10) Ω. Ternyata jembatan seimbang jika kontak C digeser 30 cm ke kanan (mengapa tidak digeser ke kiri?). Jadi,
AC sekarang = (40 + 30) cm = 70 cm
CB sekarang = (100 – 70) cm = 30 cm

Dari syarat jembatan seimbang kita peroleh:
(X + 10)CB = (Y)(AC)
(X + 10)30 cm = Y(70 cm)
3X + 30 = 7Y (**)

Masukkan nilai Y (*) ke (**), sehingga kita peroleh
3X + 30 = 7(3X/2)
2(3X + 30) = 21X
6X + 60 = 21X
–15X = –60
X = 4 Ω
Dari (*) kita peroleh Y  = (3)(4 Ω)/2 = 6 Ω