Soal dan Penyelesaian Masalah Dinamika Rotasi dan Hukum Kekekalan Energi

Soal 1
Sebuah silinder pejal homogen dengan jari-jari 20 cm sengan massa 2 kg yang berada di puncak bidang miring yang kasar pada ketinggian 1,5 m. jika silinder meluncur menuruni bidang miring dengan sudur kemiringan 30°. kelajuan silinder saat tiba di dasar bidang miring adalah . . . .
A. √3 m/s
B. √5 m/s
C. 2√2 m/s
D. 2√3 m/s 
E. 2√5 m/s

Jawab: E
Dengan menggunakan hukum kekekalan energi, kita dapat menyelesaian soal ini,

Energi mekanik di puncak bidang miring = energi mekanik di dasar bidang miring

EM_puncak = EM_dasar
EP_puncak + (EK_rotasi + EK_trans)_puncak  =  EP_dasar + (EK_rotasi + EK_trans)_dasar
Mgh + 0 = 0 + ½Iω² + ½Mv²,
Karena I = ½ MR² dan ω = v/R
Mgh = ½ (½MR²)(v/R)² + ½Mv²
gh = ¾v²
10 m/s² x 1,5 m = ¾v²
v = 2√5 m/s


Soal 2
Tersedia dua bidang miring identik. Bidang yang pertama permukaan miringnya kasar sedangkan bidang yang kedua permukaannya miringnya dianggap licin. Dalam percobaan pertama bola pejal dengan jari-jari R dilepaskan dari puncak bidang miring kasar sedangkan dalam percobaan kedua dilepaskan dari bidang miring licin. Rasio kelajuan bola di dasar bidang miring dalam percobaan pertama dan kedua adalah . . . .
A. 1
B. 2√5/5
C. √14/7
D. √6/3
E. √35/7

Jawab: E
Kita menyelesaian soal ini dengan menggunakan hukum kekekalan energi.

BIDANG MIRING KASAR (Benda bergerak tanpa slip)

Energi mekanik di puncak bidang miring = energi mekanik di dasar bidang miring
EM_puncak = EM_dasar
EP_puncak + (EK_rotasi + EK_trans)_puncak  =  EP_dasar + (EK_rotasi + EK_trans)_dasar
Mgh + 0 = 0 + ½Iω² + ½Mv²,
Karena I =  2MR²/5 dan ω = v/R
Mgh = ½ (2MR²/5)(v/R)² + ½Mv²
gh = 7v²/10 (*)

BIDANG MIRING LICIN (Benda akan slip), maka tidak ada rotasi, sehingga

EM_puncak = EM_dasar
Mgh = ½mu²
gh = ½u² (**)

maka perbandingan antara v dan u adalah
v/u = √5/√7 = √35/7

Soal 3
Sebuah bola tipis berongga dengan masa m dan jari jari r menggelinding dengan kelajuan linier v sepanjang suatu bidang horizontal tanpa tergelincir (slip). Jika momen inersia bola adalah 2mR²/3, energi kinetik bola adalah . . . . 
A. mv²/6 
B. mv²/3 
C. mv²/2
D. 2mv²/3
E. 5mv²/6

Jawab: B
Bola menggelinding maka energi kinetik bola tersebut adalah
EK_TOTAL = EK_TRANS + EK_ROTASI
EK_TOTAL = ½ mv² + ½Iω²
EK_TOTAL = ½mv² + ½(2mR²/3)(v/R)² = mv²/3

Soal 4
Sebuah bola pejal dengan jari jari R dan bermassa m didorong dengan kecepatan awal 3 m/s ke atas sebuah bidang miring yang memiliki kemiringan 30° dengan koefisien gesek kinetik 0,2 dan koefisien gesek statik 0,3. Ketika menaiki bidang tersebut, bola selalu menggelinding dan tidak pernah tergelincir. Ketinggian maksimum yang dicapai bola tersebut adalah sekitar . . . .
A. 0,006 m
B. 0,32 m
C. 0,64 m
D. 0,92 m
E. 2,32 m

Jawab: C
BIDANG MIRING KASAR (Benda bergerak tanpa slip)

Energi mekanik di puncak bidang miring = energi mekanik di dasar bidang miring
EM_puncak = EM_dasar
EP_puncak + (EK_rotasi + EK_trans)_puncak  =  EP_dasar + (EK_rotasi + EK_trans)_dasar
Mgh + 0 = 0 + ½Iω² + ½Mv²,
Karena I =  2MR²/5 dan ω = v/R
Mgh = ½ (2MR²/5)(v/R)² + ½Mv²
gh = 7v²/10
9,8 m/s² x h = 7(3 m/s)²/10
h = 0,64 m

Soal  5
Sebuah bola pejal bermassa 0,036 kg dan jari-jari 1,2 cm mengelinding menuruni suatu bidang miring. bola pejal itu mula-mula bergerak dengan kecepatan 0,50 m/s. Kecepatan bola itu ketika ketinggiannya berkurang 14 cm adalah . . . . ( percepatan gravitasi g =10 m/s²)
A. 1,0 m/s
B. 1,5 m/s
C. 2,0 m/s
D. 2,5 m/s
E. 3,0 m/s

Jawab:
bola bergerak tanpa slip, maka berlaku energi mekanik di puncak bidang miring = energi mekanik di dasar bidang miring,

EM_puncak = EM_dasar
EP_puncak + (EK_rotasi + EK_trans)_puncak  =  EP_dasar + (EK_rotasi + EK_trans)_dasar
Mgh + ½Iω₀² + ½Mv₀² = 0 + ½Iω² + ½Mv²,
Karena I =  2MR²/5 dan ω = v/R
Mgh + ½ (2MR²/5)(v₀/R)² + ½Mv₀² = ½ (2MR²/5)(v/R)² + ½Mv²
gh + 7v₀²/10 = 7v²/10
10 m/s² x 0,14 m + 7(0,5 m/s)²/10 = 7v²/10
v² = 63/28
v = 1,5 m/s

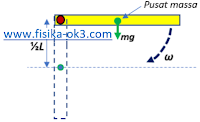
Soal 6

Sebuah batang homogen bermassa m dan panjang L diberi engsel salah satu ujungnya sehingga batang bebas berotasi. Batang dinaikkan sehingga posisinya horizontal, kemudian dibrbaskan dari keadaan diam sehingga batang berotasi terhadap suatu sumbu dalam bidang vertikal. Kecepatan sudut ketika batang tepat pada posisi vertikal adalah . . . . 
A. ω = (3g/L)^1/2 
B. ω = (2g/3L)^1/2 
C. ω = (2g/L)^1/2 
D. ω = (g/L)^1/2 
E. ω = (g/2L)^1/2

Jawab: A
Gerakan pusat massa batang berlaku hukum kekekalan energi mekanik, maka
Mgh = ½Iω²

Mg(L/2) = ½ (ML²/3)ω²
ω = (3g/L)^1/2

Soal 7
Sebuah bola bermassa M dan jari-jari R memiliki momen inersia I = 2MR²/5. Bola dibebaskan dari keadaan diam dan menggelinding menuruni bidang miring tanpa kehilangan energi karena gesekan. Bola terlempar vertikal ke atas, keluar dari bidang miring seperti ditunjukkan dalam diagram mencapai ketinggian maksimum y_maks di atas titik tempat bola meninggalkan bidang.

Ketinggian maksimum bola y_maks­ (dinyatakan dalam h) besarnya adalah . . . .

A. 2h/5
B. 25h/49
C. 5h/7 
D. h
E. 7h/5

Jawab: C
Kita menyelesaian soal ini dengan mudah menggunakan hukum kekekalan energi mekanik,

EM_puncak = EM_dasar
EP_puncak + (EK_rotasi + EK_trans)_puncak  =  EP_dasar + (EK_rotasi + EK_trans)_dasar
Mgh + 0 = 0 + ½ Iω² + ½ Mv²
Karena I =  2MR²/5 dan ω = v/R
Mgh = ½ (2MR²/5)(v/R)² + ½Mv²
gh = 7v²/10
v_dasar = (10gh/7)^1/2

bola masih akan bergerak vertikal ke atas karena memiliki energi kinetik dan sampai pada ketinggian y_maks adalah
½ Mv²_dasar = Mgy_maks
½(10gh/7) = gy_maks
y_maks = 5h/7