Pembahasan Soal Latihan UN (UNBK) Fisika 2020 (9-16)

Soal 9

Sebuah benda massanya 2 kg pada keadaan tertentu memiliki energi mekanik sebesar 90 Joule, Jika g = 10 ms^-2 , maka ketinggian benda pada saat energi kinetiknya bernilai 10 Joule adalah….

A. 4,0 m                        

B. 6,0 m
C. 7,0 m
D. 8,0 m
E. 9,0 m

Jawab: A
Massa m = 2kg, energi kinetik EM = 90J, EK = 10 J.

Kita gunakan
EM = EK + EP

90 J = 10 J + 2kg(10m.s^-2)h
h = 4 m

Soal 10

Sebuah palu bermassa 2 kg dengan kecepatan 20 m/s menghantam sebuah paku sehingga paku ini masuk ke dalam kayu 5 cm. Besar gaya gesek pada kayu adalah ….
A. 400 N

B. 800 N

C. 4000 N

D. 8000 N

E. 40000 N

Jawab:
Kita gunakan konsep, usaha total sama dengan perubahan energi kinetik.

W_nk = ∆EK

–fs = 0 – ½mv²
f(0,05m) = ½ (2kg)(20m/s)²

f = 8000 N

Soal 11
Perhatikan grafik hasil percobaan tiga buah pegas yang berbeda pada gambar (1)!

Bila ketiga pegas tersebut disusun dan diberi beban 2,5 kg seperti gambar (2), maka pertambahan panjang pada susunan pegas adalah ….
A. 3,12 cm

B. 8,89 cm

C. 11,25 cm

D. 12,50 cm

E. 33 cm

Jawab: D
Dari grafik kita peroleh konstanta masing-masing pegas, yaitu
k_A = 10N/(0,02 m) = 500N/m
k_B = 9N/(0,03 m) = 300N/m
k_C = 5N/(0,05 m) = 100N/m

Pegas A dan C disusun paralel,
k_AC = k_A + k_C = 500N/m + 100N/m = 600N/m

Maka konstanta pegas total adalah
k_T = k_Bk_AC/(k_B + k_AC)
k_T = (300N/m)(600N/m)/(900N/m) = 200N/m

Jadi, pertambahan panjang total adalah
∆x = mg/k = 25N/(200N/m) = 12.50 cm

Soal 12
Sebuah papan yang memiliki panjang 4 m ditumpu tepat di bagian tengah digunakan empat orang anak untuk bermain jungkat jungkit.

Jika massa anak yang berada di ujung kiri berturut-turut A (24 kg) dan B (26 kg) dan yang berada di ujung kanan adalah C (20 kg) dan D (22 kg), maka agar keadaan jungkat jungkit seimbang, maka posisi B harus bergeser sejauh….
A. 0,32 m
B. 0,52 m
C. 0,8 m
D. 1 m
E. 1,2 m

 

Jawab: B
Jumlah gaya di bagian kiri titik tumpuh adalah F_AB = (24kg + 26kg)(10 m/s²) = 500 N
Jumlah gaya di bagian kiri titik tumpuh adalah F_CD = (20kg + 22kg)(10 m/s²) = 420 N

 

Karena F_AB > F_CD maka anak B harus bergeser mendekati titik tumpuh sejauh x seperti gambar di bawah ini,

∑τ = 0 = –240N(2m) – 260N(x) + 200N(1,8m) + 220N(2m)

26x = 32
x = 1,23m

Karena posisi semula B berapa pada 1,75 m dari titik tumpuh maka B harus bergeser sejauh 1,75 m - 1,23 m = 0,52 m ke kiri.

Soal 13

Perhatikan gambar tiga benda berupa bola pejal (A), silinder pejal (B), dan cincin (C) menggelinding di sebuah bidang miring.
Bila momen inersia silinder pejal , momen inersia bola pejal dan momen inersia cincin maka urutan kecepatan benda saat sampai ke dasar bidang miring adalah ….
A. A, B, C
B. A, C, B
C. B, A, C
D. B, C, A
E. C, A, B

Jawab: A

Pakai hukum kekekalan energi mekanik,
mgh = EK_trans + EK_rotasi
kita peroleh
v = [2gh/(1 + β)]^1/2

Dengan momen inersia benda pejal adalah I = βmr².

Jelas bahwa benda yang momen inersianya paling kecil (atau β kecil) kecepatannya paling besar, maka dari soal ini bola pejal akan mencapai tanah lebih dahulu diikuti silinder kemudian cincin.

Soal 14
Perhatikan gambar dibawah!

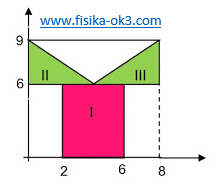
Maka kordinat titik berat terhadap sumbu x adalah . . . .
A. 11/3
B. 12/3
C. 13/3
D. 14/3
E. 15/3

Jawab: C
Luas I = 4 x 6 cm² = 24 cm²                                x₁ = 4 cm, y₁ = 3 cm
Luas II = ½ x 3 x 4 cm² = 6 cm²                         x₂ = 2 cm, y₂ = 6 + 3 x 1/3 cm = 7 cm
Luas III = ½ x 3 x 4 cm² = 6 cm²                         x₃ = 6 cm, y₃ = 6 + 3 x 1/3 cm = 7 cm

y₀ = (A₁x₁ + A₂x₂ + A₃x₃)/(A₁ + A₂ + A₃)
y₀ = [(24)(3) + (6)(7) + (6)(7)]/(36) = 13/3

Soal 15

Balok dengan ukuran 20 x 20 x 20 cm³ dimasukkan ke dalam wadah yang berisi air seperti gambar.
Balok yang muncul di atas permukaan air adalah 25% (Gb. (i)). Agar seluruh balok tepat berada di bawah permukaan balok seperti gambar (ii), maka perlu ditambahkan balok lain bermassa….
A. 8 kg
B. 12 kg
C. 16 kg
D. 20 kg
E. 25 kg

Jawab:
Dengan gambar (i) kita gunakan untuk massa jenis balok, yaitu
ρ_fV_bf = ρ_bV_b

(1000kg/m³)(0,75V_b) = ρ_bV_b
ρ_b = 750kg/m³

massa balok M  = (750 kg/m³)(8 x 10^-3 m³) = 6kg
Agar balok tercelup seluruhnya ke dalam air maka berlaku
(M_atas + M_bawah)g = ρ_fgV_bf

M_atas + 6 kg = (1000 kg/m³)(8 x 10^-3 m³)
M_­atas + 6 kg = 8 kg
M_atas = 2 kg

Soal 

Perhatikan gambar penampang sayap pesawat berikut ini!

P₂ dan v₂ adalah tekanan dan kecepatan aliran udara diatas sayap pesawat, P₁ dan v₂ adalah tekanan dan kecepatan aliran udara di bawah sayap pesawat. Agar sayap pesawat dapat mengangkat pesawat, maka…..
A. P₁ = P₂ dan v₁ = v₂
B. P₁< P₂ dan v₁> v₂
C. P₁< P₂ dan v₁< v₂
D. P₁> P₂ dan v₁> v₂
E. _P1> P₂ dan v₁< v₂

Jawab:
Agar sayap pesawat dapat terangkat ke atas harus ada perbedaan tekanan bagian bawah P₁ harus lebih besar dari tekanan bagian bawah P₂.
Tekanan berbanding terbalik dengan kecepatan aliran udara, sehingga pernyataan yang besar adalah
P₁ > P₂ dan v₁ < v₂