Soal SIMAK UI FISIKA 2011 dan Pembahasannya
Soal #25
Radioisotop K-40 digunakan untuk mengetahui umur sampel batu. Waktu paruh K-40 adalah 1, 28 × 109 tahun . Jumlah peluruhan per detik terjadi pada sampel yang mengandung 1, 63 × 10−6 gr K-40 adalah ....
(A) 0,172 peluruhan/detik
(B) 0,245 peluruhan/detik
(C) 0,316 peluruhan/detik
(D) 0,421 peluruhan/detik
(E) 0,693 peluruhan/detik
Jawab: D
Peluruhan per detik (aktivitas radioaktif) A dihitung dengan A = lN, dengan l = konstanta radioaktif, N = jumlah zat radioaktif pada saat itu.
Karena l = 0,693/T1/2
Dengan T1/2 = waktu paruh, maka
A = [0,693/T1/2] N
= [0,693/(1,28 x 109 x 3,14 x 107)](1,63 x 10-6 x 6,03 x 1023/40)
A = 0,421 peluruhan/detik
SOAL #26
Indeks bias prisma dengan sudut pembias 750 adalah 1,414. Sudut datang minimum agar cahaya dapat keluar dari sisi yang lainnya adalah ....
(A) 300
(B) 370
(C) 450
(D) 530
(E) 600
Jawab:
Saat sinar keluar dari prisma ke udara, kondisinya adalah kondisi sudut batas/sudut kritis:
Sin i2 = n2/n1
Sin i2 = 1/1,414
i2 = 450
sudut pembias prisma
b = r1 + i2
75 = r1 + 45
r1 = 300
dari udara ke dalam prisma:
n1 sin i = n2 sin r
i = 450
SOAL #27
Lempeng konduktor memiliki kerapatan muatan +σ dan bola konduktor bermassa m bermuatan +q digantungkan pada lempeng tersebut dengan benang sutera panjang l. Sudut θ yang terbentuk kecil sekali, seperti tampak pada gambar. Nilai x adalah ....
Jawab: E
Karena sudut θ sangat kecil sin θ ≈ tan θ, atau
x/l = F/mg
x = Fl/mg = qEl/mg dengan E = s/2e0, maka
x = qsl/2mge0
Soal #28
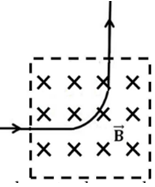
Sebuah proton bergerak dengan kecepatan 1,2 km/detik memasuki medan magnet dengan arah tegak lurus terhadap medan magnet. Proton keluar medan magnet dengan arah tegak lurus terhadap arah datangnya. Proton bergerak sejauh 3,14 cm selama di medan magnet. Besar medan magnet tersebut adalah .... (mp = 1, 6 × 10−27kg, qp = 1,6 × 10−19C)
(A) 6 × 10−4 T
(B) 6 × 10−3 T
(C) 6 × 10−2 T
(D) 3 × 10−3 T
(E) 3 × 10−2 T
Jawab:
Diketahui: kecepatan v = 1,2 km/s = 1,2 x 103 m/s, s = 3,14 cm = 3,14 x 10-2 m, massa proton mp = 1,6 x 10-27 kg dan muatan proton qp = 1,6 x 10-19 C.
s = ¼ keliling lingkaran = ¼ x 2πR
3,14 x 10-2 = ¼ x 2Πr
R = 2 x 10-2 m
Maka besarnya medan magnet kita peroleh dari
B = mv/qR
= (1,6 x 10-27)(1,2 x 103)/(1,6 x 10-19)(2 x 10-2)
B = 6 x 10-4 T
Soal #29
Benda dengan massa 2 kg dalam keadaan diam mendapat gaya F = 8i − 4tj N. Waktu yang dibutuhkan agar benda mencapai laju kecepatan 15 m/detik adalah ....
(A) 3 detik
(B) 3,5 detik
(C) 4 detik
(D) 4,5 detik
(E) 5 detik
Jawab:
Diketahui: F = 8i − 4tj N, kecepatan v = 15 m/s, massa benda = 2kg, maka percepatan yang dialami benda adalah
a = ΣF/m = 8i − 4tj N/2 kg
a = 4i − 2tj m/s2
Δv = ∫adt
Δv = 4ti – t2j
Besar Δv adalah
lΔvl2 = (4t)2 + (t2)2
152 = 16t2 + t4
t4 + 16t2 – 225 = 0
(t2 – 9)(t2 + 25) = 0
t = 3 sekon
Soal #30
Tongkat bermassa 1 kg memiliki sumbu putar tanpa gesekan pada pusat massanya, seperti pada gambar. Sebongkah tanah liat memiliki kecepatan 10 m/detik menumbuk tongkat dan tetap menempel pada tongkat. Kehilangan energi pada peristiwa ini adalah ....
(A) 1,84 joule
(B) 2,69 joule
(C) 3,84 joule
(D) 2,54 joule
(E) 1,54 joule
Jawab:
Sesaat setelah tumbukkan berlaku hukum kekekalan momentum sudut:
L = L’
mbvR = (Ib + It)ω
Dengan mb = massa tanah liat, v = kecepatan tanah liat, Ib = momen inersia tanah liat dan It = momen inersia tongkat, maka
mbvR = (mbR2 + 1/12 mtL2)ω
0,1 x 10 x 0,5 = (0,1 x 0,52 + 1/12 x 1 x 12)ω
ω = 60/13 rad/s
Perubahan energi kinetiknya:
EK = ½ mbv2 = ½ x 0,1 x 102 = 5 J
EK’ = ½ (Ib + It)ω2 = ½ (13/120)(60/13)2 = 15/13 J
Maka ΔEK = EK’ – EK = 5 J – 15/13 J = 3,84 J
Soal #31
Sebuah mesin kalor bekerja di antara reservoir dingin (T1 = 35 ◦C) dan reservoir panas (T2 = 140 ◦C). Jika mesin menyerap kalor dari reservoir panas sebesar 90 J dan membuang kalor ke reservoir dingin sebesar 150 J, maka efisiensi mesin tersebut adalah ....
(A) 75,0 %
(B) 74,6 %
(C) 40,0 %
(D) 25,4 %
(E) 25,0 %
Jawab:
Diketahui: suhu reservoir tinggi T1 = 1400C, suhu reservoir suhu rendah T2 = 350C, kalor pada reservoir suhu rendah Q2 = 90 J dan kalor pada reservoir suhu tinggi Q1 = 150 J, maka efisiensi mesin tesrbut adalah
η = (1 – T2/T1) 100% = (1 – 35/140)100% = 75%
Soal #32
Suatu benda bergetar harmonik sederhana dengan amplitude 8 cm dan frekuensi 0,5 Hz, saat energi potensial 1/3 kali energi kinetiknya, maka besar percepatan benda adalah .... (Gunakan π2 = 10 )
(A) 0,4 m/s2
(B) 0,4√2 m/s2
(C) 0, 4√3 m/s2
(D) 0,2 m/s2
(E) 0,2√2 m/s2
Jawab:
Diketahui: amplitudo A = 8 cm = 0,08 m, frekuensi f = 0,5 Hz dan Ep = Ek/3.
Percepatan benda adalah
a = ω2A[Ep/(Ep + Ek)]1/2
= (2πf)2A[Ep/(Ep + Ek)]1/2
a = (2π x 0,5)2 x 0,08/[Ep/(Ep + 3Ep)]1/2
a = 10 x 8 x 10-2 x 0,5 = 0,4 m/s2
Soal #33
Bola berada pada puncak bangunan 1/2 bola dengan radius 100 m. Bola diberi kecepatan awal agar bola tidak pernah mengenai bangunan. Nilai minimum z adalah ....
(A) 0 m
(B) 11,45 m
(C) 41,42 m
(D) 35,36 m
(E) 25,35 m
Jawab:
Diketahui: h = R dan x = R + z
Kecepatan benda v = √(gR) dan t = √(2h/g)
x = R + z = vt
R + z = √(gR) x √(2h/g)
R + z = R√2
z = R(√2 – 1) = 41,42 m
Soal #34
Pemanfaatan sinar-X dalam foto rontgen dapat pula digunakan untuk melihat cacat di dalam suatu material.
SEBAB
Sinar-X dapat merusak organ manusia bila dosisnya melebihi batas tertentu.
Jawab: B
Sinar-X memiliki frekuensi antara 1016 Hz – 1020 Hz sehingga memiliki panjang gelombang yang sangat pendek sehingga sinar X mempunyai daya tembus yang besar. Karena mempunyai daya tembus yang besar inilah maka pemanfaatan sinar-X dalam foto rontgen dapat pula digunakan untuk melihat cacat di dalam suatu material (Pernyataan benar)
Urutan spektrum gelombang elektromagnetik dari energi tinggi ke energi rendah adalah sinar Gamma, sinar X, sinar UV, sinat tampak (mejikuhibiniu), sinar infremerah, gelombang mikro, gelombang TV, gelombang radio.
Di dalam urutan spektrum gelombang elektromagnetik, sinar-X memiliki urutan energi tinggi setelah sinar gamma sehingga sinar-X dapat merusak organ manusia bila dosisnya melebihi batas tertentu (alasannya benar)
TIDAK ADA HUBUNGAN ANTARA PERNYATAAN DAN ALASAN!
Soal #35
Dua buah piringan logam memiliki massa yang sama M dan ketebalan yang sama t. Rapat massa piringan pertama ρ1 lebih kecil daripada rapat massa piringan kedua ρ2. Maka momen inersia piringan pertama I1 lebih kecil daripada momen inersia piringan kedua I2.
SEBAB
Momen inersia suatu benda secara substansial bergantung kepada rapat massanya.
Jawab: D
Diketahui: m1 = m2 = m dan t1 = t2 = t dan ρ1 = ρ2, dengan ρ = m/V = 3m/4πR3,
Maka ρ ≈ 1/R3, sehingga R1 > R2
Soal #36
Bulan memiliki stabilitas orbit dan setia tidak meninggalkan bumi karena bulan memiliki ....
(1) momentum sudut total konstan
(2) energi total konstan bernilai positif
(3) energi total konstan bernilai negatif
(4) energi total sama dengan nol
Jawab: B
Pada bulan yang bergerak mengelilingi bumi, terjadi gerak melingkar dan gaya gravitasi,
(1) Pada benda yang bergerak melingkar, momentum sudut bida dihitung menggunakan rumus L = mω2.R karena massa bulan (m) konstan, periode bulan (T) mengelilingi bumi juga konstan maka ω akan bernilai konstan. Demikian juga dengan jarak bumi bulan R kostan maka nilai momentum sudut L konstan maka nilai momentum sudut akan konstan (pernyataan (1) benar)
(2) E = EK + EP = - GMm/R (energi bernilai negatif) (pernyataan (2) salah)
(3) E = EK + EP = - GMm/R (energi bernilai negatif) (pernyataan (3) benar)
(4) E = EK + EP = - GMm/R (energi bernilai negatif bukan nol) (pernyataan (4) salah)
Soal #25
Radioisotop K-40 digunakan untuk mengetahui umur sampel batu. Waktu paruh K-40 adalah 1, 28 × 109 tahun . Jumlah peluruhan per detik terjadi pada sampel yang mengandung 1, 63 × 10−6 gr K-40 adalah ....
(A) 0,172 peluruhan/detik
(B) 0,245 peluruhan/detik
(C) 0,316 peluruhan/detik
(D) 0,421 peluruhan/detik
(E) 0,693 peluruhan/detik
Jawab: D
Peluruhan per detik (aktivitas radioaktif) A dihitung dengan A = lN, dengan l = konstanta radioaktif, N = jumlah zat radioaktif pada saat itu.
Karena l = 0,693/T1/2
Dengan T1/2 = waktu paruh, maka
A = [0,693/T1/2] N
= [0,693/(1,28 x 109 x 3,14 x 107)](1,63 x 10-6 x 6,03 x 1023/40)
A = 0,421 peluruhan/detik
SOAL #26
Indeks bias prisma dengan sudut pembias 750 adalah 1,414. Sudut datang minimum agar cahaya dapat keluar dari sisi yang lainnya adalah ....
(A) 300
(B) 370
(C) 450
(D) 530
(E) 600
Jawab:
Saat sinar keluar dari prisma ke udara, kondisinya adalah kondisi sudut batas/sudut kritis:
Sin i2 = n2/n1
Sin i2 = 1/1,414
i2 = 450
sudut pembias prisma
b = r1 + i2
75 = r1 + 45
r1 = 300
dari udara ke dalam prisma:
n1 sin i = n2 sin r
- sin r = 1,414 sin 300
i = 450
SOAL #27
Lempeng konduktor memiliki kerapatan muatan +σ dan bola konduktor bermassa m bermuatan +q digantungkan pada lempeng tersebut dengan benang sutera panjang l. Sudut θ yang terbentuk kecil sekali, seperti tampak pada gambar. Nilai x adalah ....
Jawab: E
Karena sudut θ sangat kecil sin θ ≈ tan θ, atau
x/l = F/mg
x = Fl/mg = qEl/mg dengan E = s/2e0, maka
x = qsl/2mge0
Soal #28
Sebuah proton bergerak dengan kecepatan 1,2 km/detik memasuki medan magnet dengan arah tegak lurus terhadap medan magnet. Proton keluar medan magnet dengan arah tegak lurus terhadap arah datangnya. Proton bergerak sejauh 3,14 cm selama di medan magnet. Besar medan magnet tersebut adalah .... (mp = 1, 6 × 10−27kg, qp = 1,6 × 10−19C)
(A) 6 × 10−4 T
(B) 6 × 10−3 T
(C) 6 × 10−2 T
(D) 3 × 10−3 T
(E) 3 × 10−2 T
Jawab:
Diketahui: kecepatan v = 1,2 km/s = 1,2 x 103 m/s, s = 3,14 cm = 3,14 x 10-2 m, massa proton mp = 1,6 x 10-27 kg dan muatan proton qp = 1,6 x 10-19 C.
s = ¼ keliling lingkaran = ¼ x 2πR
3,14 x 10-2 = ¼ x 2Πr
R = 2 x 10-2 m
Maka besarnya medan magnet kita peroleh dari
B = mv/qR
= (1,6 x 10-27)(1,2 x 103)/(1,6 x 10-19)(2 x 10-2)
B = 6 x 10-4 T
Soal #29
Benda dengan massa 2 kg dalam keadaan diam mendapat gaya F = 8i − 4tj N. Waktu yang dibutuhkan agar benda mencapai laju kecepatan 15 m/detik adalah ....
(A) 3 detik
(B) 3,5 detik
(C) 4 detik
(D) 4,5 detik
(E) 5 detik
Jawab:
Diketahui: F = 8i − 4tj N, kecepatan v = 15 m/s, massa benda = 2kg, maka percepatan yang dialami benda adalah
a = ΣF/m = 8i − 4tj N/2 kg
a = 4i − 2tj m/s2
Δv = ∫adt
Δv = 4ti – t2j
Besar Δv adalah
lΔvl2 = (4t)2 + (t2)2
152 = 16t2 + t4
t4 + 16t2 – 225 = 0
(t2 – 9)(t2 + 25) = 0
t = 3 sekon
Soal #30
Tongkat bermassa 1 kg memiliki sumbu putar tanpa gesekan pada pusat massanya, seperti pada gambar. Sebongkah tanah liat memiliki kecepatan 10 m/detik menumbuk tongkat dan tetap menempel pada tongkat. Kehilangan energi pada peristiwa ini adalah ....
(A) 1,84 joule
(B) 2,69 joule
(C) 3,84 joule
(D) 2,54 joule
(E) 1,54 joule
Jawab:
Sesaat setelah tumbukkan berlaku hukum kekekalan momentum sudut:
L = L’
mbvR = (Ib + It)ω
Dengan mb = massa tanah liat, v = kecepatan tanah liat, Ib = momen inersia tanah liat dan It = momen inersia tongkat, maka
mbvR = (mbR2 + 1/12 mtL2)ω
0,1 x 10 x 0,5 = (0,1 x 0,52 + 1/12 x 1 x 12)ω
ω = 60/13 rad/s
Perubahan energi kinetiknya:
EK = ½ mbv2 = ½ x 0,1 x 102 = 5 J
EK’ = ½ (Ib + It)ω2 = ½ (13/120)(60/13)2 = 15/13 J
Maka ΔEK = EK’ – EK = 5 J – 15/13 J = 3,84 J
Soal #31
Sebuah mesin kalor bekerja di antara reservoir dingin (T1 = 35 ◦C) dan reservoir panas (T2 = 140 ◦C). Jika mesin menyerap kalor dari reservoir panas sebesar 90 J dan membuang kalor ke reservoir dingin sebesar 150 J, maka efisiensi mesin tersebut adalah ....
(A) 75,0 %
(B) 74,6 %
(C) 40,0 %
(D) 25,4 %
(E) 25,0 %
Jawab:
Diketahui: suhu reservoir tinggi T1 = 1400C, suhu reservoir suhu rendah T2 = 350C, kalor pada reservoir suhu rendah Q2 = 90 J dan kalor pada reservoir suhu tinggi Q1 = 150 J, maka efisiensi mesin tesrbut adalah
η = (1 – T2/T1) 100% = (1 – 35/140)100% = 75%
Soal #32
Suatu benda bergetar harmonik sederhana dengan amplitude 8 cm dan frekuensi 0,5 Hz, saat energi potensial 1/3 kali energi kinetiknya, maka besar percepatan benda adalah .... (Gunakan π2 = 10 )
(A) 0,4 m/s2
(B) 0,4√2 m/s2
(C) 0, 4√3 m/s2
(D) 0,2 m/s2
(E) 0,2√2 m/s2
Jawab:
Diketahui: amplitudo A = 8 cm = 0,08 m, frekuensi f = 0,5 Hz dan Ep = Ek/3.
Percepatan benda adalah
a = ω2A[Ep/(Ep + Ek)]1/2
= (2πf)2A[Ep/(Ep + Ek)]1/2
a = (2π x 0,5)2 x 0,08/[Ep/(Ep + 3Ep)]1/2
a = 10 x 8 x 10-2 x 0,5 = 0,4 m/s2
Soal #33
Bola berada pada puncak bangunan 1/2 bola dengan radius 100 m. Bola diberi kecepatan awal agar bola tidak pernah mengenai bangunan. Nilai minimum z adalah ....
(A) 0 m
(B) 11,45 m
(C) 41,42 m
(D) 35,36 m
(E) 25,35 m
Jawab:
Diketahui: h = R dan x = R + z
Kecepatan benda v = √(gR) dan t = √(2h/g)
x = R + z = vt
R + z = √(gR) x √(2h/g)
R + z = R√2
z = R(√2 – 1) = 41,42 m
Soal #34
Pemanfaatan sinar-X dalam foto rontgen dapat pula digunakan untuk melihat cacat di dalam suatu material.
SEBAB
Sinar-X dapat merusak organ manusia bila dosisnya melebihi batas tertentu.
Jawab: B
Sinar-X memiliki frekuensi antara 1016 Hz – 1020 Hz sehingga memiliki panjang gelombang yang sangat pendek sehingga sinar X mempunyai daya tembus yang besar. Karena mempunyai daya tembus yang besar inilah maka pemanfaatan sinar-X dalam foto rontgen dapat pula digunakan untuk melihat cacat di dalam suatu material (Pernyataan benar)
Urutan spektrum gelombang elektromagnetik dari energi tinggi ke energi rendah adalah sinar Gamma, sinar X, sinar UV, sinat tampak (mejikuhibiniu), sinar infremerah, gelombang mikro, gelombang TV, gelombang radio.
Di dalam urutan spektrum gelombang elektromagnetik, sinar-X memiliki urutan energi tinggi setelah sinar gamma sehingga sinar-X dapat merusak organ manusia bila dosisnya melebihi batas tertentu (alasannya benar)
TIDAK ADA HUBUNGAN ANTARA PERNYATAAN DAN ALASAN!
Soal #35
Dua buah piringan logam memiliki massa yang sama M dan ketebalan yang sama t. Rapat massa piringan pertama ρ1 lebih kecil daripada rapat massa piringan kedua ρ2. Maka momen inersia piringan pertama I1 lebih kecil daripada momen inersia piringan kedua I2.
SEBAB
Momen inersia suatu benda secara substansial bergantung kepada rapat massanya.
Jawab: D
Diketahui: m1 = m2 = m dan t1 = t2 = t dan ρ1 = ρ2, dengan ρ = m/V = 3m/4πR3,
Maka ρ ≈ 1/R3, sehingga R1 > R2
Soal #36
Bulan memiliki stabilitas orbit dan setia tidak meninggalkan bumi karena bulan memiliki ....
(1) momentum sudut total konstan
(2) energi total konstan bernilai positif
(3) energi total konstan bernilai negatif
(4) energi total sama dengan nol
Jawab: B
Pada bulan yang bergerak mengelilingi bumi, terjadi gerak melingkar dan gaya gravitasi,
(1) Pada benda yang bergerak melingkar, momentum sudut bida dihitung menggunakan rumus L = mω2.R karena massa bulan (m) konstan, periode bulan (T) mengelilingi bumi juga konstan maka ω akan bernilai konstan. Demikian juga dengan jarak bumi bulan R kostan maka nilai momentum sudut L konstan maka nilai momentum sudut akan konstan (pernyataan (1) benar)
(2) E = EK + EP = - GMm/R (energi bernilai negatif) (pernyataan (2) salah)
(3) E = EK + EP = - GMm/R (energi bernilai negatif) (pernyataan (3) benar)
(4) E = EK + EP = - GMm/R (energi bernilai negatif bukan nol) (pernyataan (4) salah)





Post a Comment for "Soal SIMAK UI FISIKA 2011 dan Pembahasannya"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!