Contoh soal penerapan hukum Newton pada sistem beban, tali dan katrol

Soal 1
Tentukan percepatan sistem pada gambar berikut. Anggap bahwa balok m₁ = 2 kg, balok m₂ = 4 kg, dan balok m₃ = 5 kg. Katrol dan bagian atas meja tersebut tanpa gesekan.

Jawab:
Diketahui: m₁ = 2 kg, m₂ = 4 kg, m₃ = 5 kg
Gaya-gaya yang bekerja pada masing-masing benda ditunjukkan pada gambar di bawah ini,

Misalkan arah gerak sistem benda seperti ditunjukkan pada gambar di atas, maka semua gaya yang berlawanan dengan arah gerak tersebut bernilai negatif.
Pada benda 1 berlaku hukum II Newton,
∑F₂ = ma
T₁₂ – m₁g = m₁a
T₁₂ – 20 = 2a
T₁₂ = 2a + 20 (*)
Pada benda 2 berlaku hukum II Newton,
∑F₂ = m₂a
T₂₃ – T₁₂ = m₂a dari (*)
T₂₃ – (2a + 20) = 4a
T₂₃ = 6a + 20 (**)
Pada benda 3 berlaku hukum II Newton,
∑F₃ = m₃a
m₃g – T₂₃ = m₃a  dari (**)
50 – (6a + 20) = 5a
30 = 11a
a = 30/11 = 2,73 m.s^-2

Soal 2
Untuk sistem seperti gambar di bawah ini, jika semua permukaan licin dan anggap katrol dan tali tidak bermassa. Tentukan: (a) hubungan antara percepatan massa balok M (a₁) dan 2M (a₂), (b) besar percepatan a₁ dan a₃ dan (c) besar tegangan tali yang melewati katrol!

Jawab:
Gaya-gaya yang bekerja pada masing-masing benda diberikan pada gambar di bawah ini,

(a) Perhatikan gambar, jika benda M bergeser sejauh x benda 2M akan bergeser sejauh x/2 dan oleh  karena percepatan sebanding dengan jarak tempuh maka a₁ = a₂/2 atau a₂ = 2a₁
(b) nilai a₁ dan a₂ kita peroleh dengan meninjauh gaya yang bekerja pada masing-masing benda
Tinjau massa 2M:
∑F₂ = m₂a₂
–2T + (2Mg) = 2Ma₂
–2T + (2Mg) = 4Ma₁

T = Mg – 2Ma₁  (*)
Tinjau massa M:
∑F₁ = Ma₁
T + (–Mg sin 30⁰) = Ma₁
T + (–0,5Mg) = Ma₁ dari (*)
Mg – 2Ma₁  = 0,5Mg + Ma₁
3a₁ = 0g
a₁ = g/6
dan a₂ = 2a₁ = g/3
(c) tegangan tali T adalah
T = Mg – 2Ma₁
   = Mg – 2M(g/6)
T = 2Mg/3

Soal 3

Pada sistem seperti gambar di bawah ini, jika semua permukaan licin dan anggap katrol dan tali tidak bermassa. Tentukan: (a) hubungan antara percepatan massa balok A dan B, (b) besar percepatan a_A dan a_B dan (c) besar tegangan tali yang melewati katrol!

Jawab:
Gaya-gaya yang bekerja pada masing-masing benda ditunjukkan pada gambar di bawah ini

(a) Perhatikan gambar, jika benda m_A bergeser sejauh x₁ benda m_C akan turun sejauh x₁/2 dan jika benda m_B bergeser sejauh x₂ benda m_C akan turun sejauh x₂/2 oleh  karena percepatan sebanding dengan jarak tempuh maka a_c = a_A/2 + a_B/2
(b) nilai a_A, a_B dan a_C kita peroleh dengan meninjauh gaya yang bekerja pada masing-masing benda
Tinjau massa m_A:
∑F_A = m_Aa_A
T = a_A   (*)
Tinjau massa m_B:
∑F_B = m_Ba_B
T = 2a_B   (**)
Tinjau benda m_C:
∑F_c = m_ca_B
–2T + m_Cg = m_Ca_C
–2T + 40 = 4a_C (***)
Dari (*) dan (**),
a_A = 2a_B maka dari a_c = a_A/2 + a_B/2       2a_C = 3a_B
a_C = 3a_B/2
sehingga (***) menjadi
–2T + 40 = 4(3a_B/2) = 6a_A dari (**)
–2(2a_B) + 40 = 6a_B
40 = 10a_B
a_B = 4,0 m.s^-2; a_c = 3 x 4/2 = 6,0 m.s^-2 dan a_A = 2a_B = 8,0 m.s^-2
 (c) tegangan tali T adalah
T = a_A = 8,0 N

Soal 4
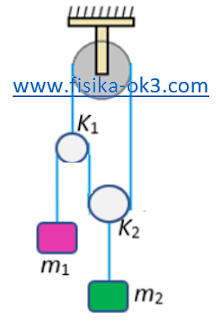
Balok m₁ = m₂ dihubungkan dalam sistem di bawah ini. Jika massa katrol licin dan tali abaikan. Tentukan percepatan massa m₁ dan m₂ dan tegangan tali dalam sistem tersebut!

Jawab
Gaya-gaya yang bekerja pada setiap benda ditunjukkan pada gambar di bawah ini

Untuk benda 1 berlaku:
∑F₁ = m₁a₁
T – m₁g = m₁a₁
T – mg = ma₁ (*)
Untuk benda 2 berlaku:
∑F₂ = m₂a₁
mg – T₂ = ma₂  (**)
Tinjau katrol K₂: T₂ = 2T, maka (**) menjadi
mg – 2T = ma₂ (***)
dari (*) dan (***) kita peroleh
–g = 2a₁ + a₂
Dari gambar kita dapatkan a₁ = –a₂, maka
–g = –2a₂ + a₂
a₂ = g = 9,8 m.s^-2
dan a₁ = –a₂ = –g = –9,8 m.s^-2