Soal Grafik Gerak Lurus dan Pembahasan

Soal 1
Gambar di atas merupakan grafik posisi terhadap waktu dari sebuah mobil yang sedang bergerak pada arah horisontal. Gambarlah grafik kecepatan terhadap waktu untuk gerakan mobil ini!

Jawab:
Ingat bahwa kecepatan (= Δposisi/Δwaktu) mewakili kemiringan grafik posisi-waktu. Kemiringan konstan (garis lurus) pada grafik posisi-waktu melambangkan garis datar pada grafik kecepatan-waktu, dan kemiringan yang berubah pada grafik posisi-waktu akan merepresentasikan perubahan kecepatan, peningkatan kecepatan untuk kurva posisi-waktu ke atas cekung , dan penurunan kecepatan untuk kurva posisi-waktu cekung-bawah.
Grafik kecepatan terhadap waktu yang tepat adalah seperti di bawah ini,

Soal 2
Empat grafik posisi-waktu dari gerak linear mobil mainan A, B, C dan D yang ditunjukkan dalam gambar.

(a) Jelaskan secara verbal gerakan setiap mobil.

(b) Tentukan kecepatan rata-rata setiap mobil pada interval dari 0 detik hingga 4 detik.
(c) Tentukan kecepatan sesaat dari setiap mobil pada t = 4 dtk.
(d) Dalam satu gambar, gambarlah grafik kecepatan-waktu untuk setiap mobil.
(e) Tentukan total perpindahan pada setiap t₁ = 10 detik mobil (termasuk pemindahan awal tanpa nol, jika ada), asalkan gerakan berlanjut dengan ketergantungan waktu yang sama seperti yang ditunjukkan pada gambar.

Jawab:
(a) Grafik A: Perpindahan mobil A tidak berubah pada waktunya. Mobil sedang beristirahat (diam). Perpindahan awal adalah 10 m.
Grafik B: Perpindahan meningkat secara linier terhadap waktu. Kecepatan gerak tidak berubah. Mobil bergerak dalam gerak lurus konstan (GLB) dengan perpindahan awal sebesar 4 m.
Grafik C: Perpindahan meningkat secara linier terhadap waktu. Kecepatan gerak tidak berubah. Mobil bergerak dalam gerakan lurus tetap dengan perpindahan awal sama dengan nol.
Grafik D: Perpindahan dapat dinyatakan secara matematis sebagai parabola - skala perpindahan secara kuadratis dengan waktu. Ini mengikuti bahwa skala kecepatan secara linear dengan waktu. Mobil bergerak dalam gerakan linier dipercepat dengan kecepatan bertambah secara konstan dengan perpindahan awal sama dengan nol.
(b) Kecepatan rata-rata v ditentukan oleh perbandingan perpindahan dengan interval waktu yang sesuai 4 s:
A: perpindahan s₄ = 0, v_p = 0
B: perpindahan s₄ = 6m, v_p = 64 m⋅s⁻¹ = 1.5 m⋅s⁻¹
C: perpindahan s₄ = 10 m, v_p = 104 ms⁻¹ = 2.5 m⋅s⁻¹
D: perpindahan s₄ = 10 m, v_p = 104 m⋅s⁻¹ = 2.5 m⋅s⁻¹.
(c) Grafik A, B, C: Kecepatan tidak berubah seiring waktu. Kecepatan sesaat karena itu sama dengan kecepatan rata-rata yang dihitung dalam (b).
Kecepatan diberikan oleh kemiringan garis.
Grafik D:
Perpindahan gerakan linear dipercepat seragam diberikan oleh rumus
s = ½ at²
(Perpindahan dan kecepatan pada waktu t = 0 s sama dengan nol.)
Dapat dilihat dalam grafik:
Perpindahan pada saat t = 4 s adalah s(4) = 10 m
Kita mendapatkan:

10 = ½ a(4)
a = 1,25 m.s^-2
Dan untuk kecepatan sesaat:
v = at = 1,25 x 4 = 5,0 m.s^-1
(d) Memiliki jawaban atas pertanyaan sebelumnya sekarang kita tahu bagaimana kecepatan setiap gerakan berubah seiring waktu dan kita tahu nilainya pada waktu tertentu.

Sekarang kita hanya perlu memplot grafik.

Kecepatan mobil A, B, C tidak berubah seiring waktu:
Gerak mobil A: v_A = 0
Gerak mobil B: v_B = 1,5 m⋅s⁻¹
Gerak mobil C: v_C = 2.5 m⋅s⁻¹
Gerak mobil D: dari grafik kecepatan-waktu v_D = 5,0 m.s^-
Grafik kecepatan gerak setiap mobil seperti ditunjukkan di atas.

(e) Dari grafik s(t) kita menemukan nilai perpindahan untuk t = t₁ = 10 dtk.
A: Mobil masih dalam keadaan istirahat:
s₀ = s₁ = 10 m.
B: Mobil bergerak dalam lurus tetap dengan perpindahan awal nol:
s₁ = s₀ + v_Bt₁ = (4 + 1.5 x 10) m = 19 m.
C: Mobil bergerak dalam gerakan lurus tetap dengan perpindahan awal sama dengan nol:
s₁ = v_Ct₁ = (2.5 x 10) m = 25 m.
D: Mobil bergerak dalam gerakan lurus dengan percepatan tetap dengan perpindahan awal sama dengan nol:
s₁ = ½ at₁² = (1,25 x 100)/2 m = 62,5 m.

Soal 3

Variasi waktu posisi x (t) dari sangkar angkat ditunjukkan pada gambar.
(a) Jelaskan bagaimana gerakan lift itu.
(b) Gambarkan grafik kecepatan terhadap waktu dari gerakan lift.
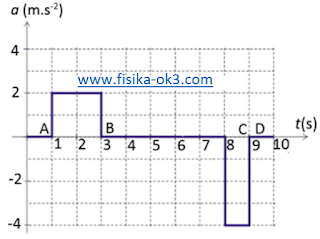
(c) Gambarkan grafik percepatan terhadap waktu dari gerakan lift.
Titik A: posisi x = 0 m pada waktu t = 1 dtk
Titik B: posisi x = 4 m pada waktu t = 3 dtk
Titik C: posisi x = 24 m pada waktu t = 8 dtk
Titik D: posisi x = 27 m pada waktu t = 9 dtk

Jawab:
(a) Mula-mula lift berdiri di bawah dan dengan demikian itu sedang diam - dalam grafik itu adalah garis antara titik asal koordinat dan titik A. Kemudian lift naik (arah positif dari sumbu koordinat), bergerak dengan percepatan konstan sampai dengan kecepatan yang pasti - dalam grafik itu adalah garis antara titik A dan titik B. Lift bergerak pada kecepatan konstan ini selama waktu yang pasti (gerakan dengan kecepatan konstan) - dalam grafik itu adalah garis antara titik B dan titik C. Pada akhirnya lift mulai melambat - dalam grafik itu adalah garis antara titik C dan titik D. Kurva dari titik D berarti bahwa lift sedang beristirahat (diam) lagi.

(b) Grafik kecepatan terhadap waktu dari gerakan lift
Fungsi v(t) adalah turunan dari fungsi s(t):
v(t) = ds/dt
Bagian dari grafik sebelum titik A dan setelah titik D sesuai dengan situasi ketika lift sedang diam. Grafik fungsi s(t) di bagian ini adalah garis sejajar dengan sumbu waktu. Gradien sudut tangen (dan juga kecepatan lift) sama dengan nol.
Antara titik B dan C lift bergerak dengan kecepatan konstan, yang kita tentukan sebagai gradien sudut dari garis BC:
v = Δs/Δt = (24 − 4)m/(8 − 3) s = 4 m.s^-1

Titik A: posisi x = 0 m pada waktu t = 1 dtk

Titik B: posisi x = 4 m pada waktu t = 3 dtk
Titik C: posisi x = 24 m pada waktu t = 8 dtk
Titik D: posisi x = 27 m pada waktu t = 9 dtk
Kecepatan lift berubah pada awal gerakan (bagian AB) dan berulang lagi pada bagian CD, yaitu dalam interval waktu dari 1 detik hingga 3 detik dan dari 8 detik hingga 9 detik. Jika kita menganggap bahwa saat mulai lift naik dan berhenti secara tetap, variasi waktu dari kecepatan akan menjadi linier (garis AB dan CD).
Variasi waktu dari kecepatan lift digambarkan dalam grafik berikut:

(c) Grafik percepatan terhadap waktu dari gerakan lift.