Pada percobaan Quincke di dalam pipa diisi udara (kecepatan bunyi di udara 340 m/s dan frekuensi sumber getarnya 440 Hz. Berapakah selisih panjang pipa variabel (yang dapat digerakan) dengan panjang pipa tetap jika (a) fase gelombang yang berinterferensi berbeda λ/4, (b) terjadi interferensi konkruktif dan (c) terjadi interferensi deskruktif.
(a) Misalkan selisih waktu antara gelombang yang merambat melalui pipa yang variabel dan tetap adalah = Δt. Anggap selisih panjang lintasan kedua gelombang yang berinterferensi (= selisih panjang kedua pipa) adalah Δx. Jika cepat rambat gelombang v maka Δx dapat dicari dengan
Δφ = Δt/T = (Δx/v)/T
Δφ = Δx/(vT)
Δφ = Δx/λ
Maka
Δx = Δφ.λ = ¼ (340 m/s/440 Hz) = 17/88 m
(b) besar Δx ketika terjadi interferensi saling menguatkan (konkruktif) adalah
Δx = (n + 1)λ/2 = (n + 1)v/2f , dengan (n = 0, 1, 2, 3, . . . , )
= (n + 1)(340 m/s)/2(440 Hz) = 17/44 m; 51/44 m, . . . dst
(b) besar Δx ketika terjadi interferensi saling melemahkan (deskruktif) adalah
Δx = nλ = nv/f , dengan (n = 0, 1, 2, 3, . . . , )
= n(340 m/s)/(440 Hz) = 0, 17/22 m; 34/22 m, . . . dst
Soal 2
Pada percobaan Quincke frekuensi sumber getarnya 340 Hz. Kecepatan bunyi di udara 340 m/s. Berapakah kita harus menggeser pipa yang variabel (yang dapat digeser) agar selisih fase gelombang yang berinterferensi naik dari ¼ menjadi ½.
Jawab:
Misalkan selisih panjang kedua pipa ketika beda fasenya Δφ1 = ¼ adalah Δx1 dan selisih panjang kedua pipa ketika beda fasenya Δφ2 = ½ adalah Δx2, pada gambar tampak bahwa
Δx1 = BCA – BEA dan Δx2 = BDA – BEA
Perubahan beda lintasan ADB dan ACB adalah 2xd di mana xd = CD adalah bagian variabel yang harus digeser, maka
2xd = Δx2 – Δx1
2xd = Δφ2λ – Δφ1λ
= (1/2 – 1/4)v/f = ¼ (340/340) = ¼
xd = 1/8 m
Soal 3
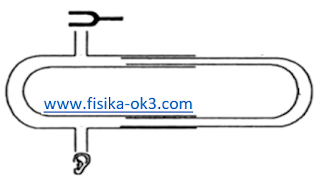
Interferometer bunyi seperti gambar di samping dijalankan oleh sebuah pengeras suara yang memancarkan frekuensi 500 Hz. Cepat rambat bunyi di udara 340 m/s. Jika interferensi destruktif terjadi pada suatu saat tertentu, berapa jauh pipa U harus digeser agar terdengar: (a) interferensi konstruktif dan (b) interferensi destruktif sekali lagi.
Frekuensi bunyi, f = 500 Hz, kecepatan rambat bunyi di udara, v = 340 m/s, maka panjang gelombang bunyi adalah λ = v/f = (340 m/s)/(500 Hz) = 17/25 m = 68 cm
(a) Interferensi konkruktif terjadi jika r2 – r1 = nλ
Jadi, interferensi konkruktif terjadi untuk
r2 – r1 = λ, 2λ, 3λ, ...., = 68 cm, 136 cm, 204, cm . . . .
Jadi, agar terjadi interferensi maksimum, beda jarak lintasan gelombang pada kedua pipa harus memenuhi,
Δr = 68 cm, 136 cm, 204, cm . . . .
Agar terjadi interferensi konkruktif ke- 1, maka
r2 – r1 = 68 cm
r2 = 68 cm + r1
artinya pipa U bagian atas harus digeser ke atas sejauh 68 cm/2 = 34 cm
begitupula dengan interferensi konkruktif ke-2, maka pipa U harus digeser sejauh 136 cm/2 = 68 cm dan seterusnya.
Jadi, secara umum, agar terjadi interferensi konkruktif, maka pipa U harus di geser sejauh
Δr = nλ/2
(b) Interferensi deskruktif terjadi jika r2 – r1 = (n – ½)λ
Jadi, interferensi deskruktif terjadi untuk
r2 – r1 = ½ λ, 3λ2, 5λ/2, ....,
karena λ = 68 cm, maka
r2 – r1 = 34 cm, 102 cm, 170, cm . . . .
Jadi, agar terjadi interferensi minimum, beda jarak lintasan gelombang pada kedua pipa harus memenuhi,
Δr = 34 cm, 102 cm, 170, cm . . . .
Agar terjadi interferensi deskruktif ke- 1, maka
r2 – r1 = 34 cm
r2 = 34 cm + r1
artinya pipa U bagian atas harus digeser ke atas sejauh 34 cm/2 = 17 cm
begitupula dengan interferensi konkruktif ke-2, maka pipa U harus digeser sejauh 102 cm/2 = 51 cm dan seterusnya.
Jadi, secara umum, agar terjadi interferensi konkruktif, maka pipa U harus di geser sejauh
Δr = (n – ½)λ/2
Soal 4
Dua pengeras suara yang koheren, P dan Q, di pisahkan pada jarak 6,0 m. Seorang pendengar berada sejauh 8,0 m dari pengeras suara Q. Segitiga PQR adalah segitiga siku-siku. Kedua pengeras suara mengeluarkan bunyi frekuenasi sama 100 Hz, dan cepat rambat bunyi di udara adalah 340 m/s. Apakah pendengar mendengar bunyi kuat atau sama sekali tidak mendengar bunyi?
Pendengar mendengar bunyi kuat atau sama sekali tak mendengar bunyi di R bergantung apakah di R terjadi interferensi konstruktif atau destruktif. Interferensi konstruktif atau destruktif ditentukan oleh hubungan beda lintasan Δs = PR – QR terhadap panjang gelombang bunyi λ.
Jawab:
Perhatikan segitiga siku-siku PQR,
PR2 = PQ2 + QR2
= (6,0 m)2 + (8,0 m)2
PR = 10,0 m
Beda lintasan kedua gelombang bunyi yang bertemu di R adalah
Δs = PR – QR = 10,0 m – 8,0 m = 2,0 m
Sekarang mari kita hitung panjag gelombang bunyi, λ, dengan persamaan dasar gelombang.
v = λf ↔ λ = v/f = 6,0 m
Δs = 2,0 = λ/3, maka
Δs = λ/3
Jadi, ketika Δs = λ/3 akan terjadi interferensi deskruktif dan pendengar akan mendengar bunyi yang lemah atau sama sekali tidak mendengar bunyi.






0Comments
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!