Soal 1
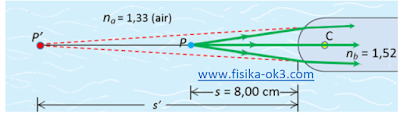
Sebuah batang gelas berbentuk silinder dalam udara (Gambar 1) mempunyai indek bias 1,52. Satu ujung gerinda (digosok) menjadi berbentuk setengah bola dengan jari-jari R = 2,00 cm, (a) Carilah jarak bayangan dari sebuah benda kecil pada sumbu batang itu, 8,00 cm di sebelah kiri dari verteks. (b) Carilah perbesaran lateral dan (c) bagaimana jika batang gelas dicelupkan dalam air yang memiliki indeks bias 1,33 tentukan jarak bayangan dan pembesaran lateralnya!
Jawab:
Kita beri na = 1,00 (udara), nb = 1,52, R = +2,00 cm, dan s = +8,00 cm
(a) dengan menggunakan
na/s + nb/s’ = (nb – nb)/R
kita peroleh
(1,00/8,00 cm) + (1,52/s’) = (1,52 – 1,00)/+2,00 cm
s' = +11,3 cm
karena s’ positif, ini berarti bayangan itu terbentuk 11,3 cm di sebelah kanan dari verteks
M = –nas’/nbs
Kita peroleh
M = –(1,00 x 11,3 cm)/(1,52 x 8,00 cm) = –0,929
Bayangan menjadi agak lebih kecil dari benda tersebut, dan bayangan terbalik. Jika benda tersebut adalah sebuah panah yang tingginya 1,000 mm yang menunjuk ke atas, maka bayangannya adalah sebuah panah yang tingginya 0,929 mm, menunjuk ke bawah.
(c) Jika batang gelas dicelupkan dalam air, gambar bayangannya seperti gambar 2.
na/s + nb/s’ = (nb – nb)/R
(1,33/8,00 cm) + (1,52/s’) = (1,52 – 1,33)/+2,00 cm
s' = –21,3 cm
nilai negatif dari s’ berti bahwa setelah sinar-sinar itu dibiaskan oleh permukaan tersebut, sinar-sinar itu tidak mengumpul tetapi terlihat terpencar dari sebuah titik 21,3 cm di sebelah kiri verteks tersebut, (membentuk sebuah bayangan maya 21,3 cm)
pembesaran lateralnya adalah
M = –(1,33 x –21,3 cm)/(1,52 x 8,00 cm) = +2,33
Dalam kasus ini bayangan itu tegak (karena M positif) dan 2,33 kali besarnya benda itu.
Soal 2
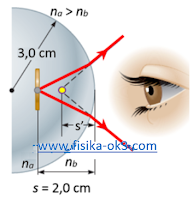
Satu koin tertanam dalam bola kertas plastik bulat memiliki radius 3,0 cm. Indeks pembiasandari plastik adalah na = 1,50. Koin berada 2,0 cm dari tepi bola (Gambar 3). Tentukan posisi bayangan koin.
Jawab:
Sketsa jalannya sinar ditunjukkan pada gambar 3. Dengan menggunakan
na/s + nb/s’ = (nb – nb)/R
kita peroleh
(1,50/2,0 cm) + (1,00/s’) = (1,00 – 1,5)/–3,0 cm
s' = –1,7 cm
Soal 3
Pemilik kolam renang mengetahui bahwa kolam selalu terlihat lebih dangkal daripada kedalaman sebenarnya dan penting untuk mengidentifikasi bagian-bagian yang dalam secara menyolok sehingga orang yang tak dapat berenang tidak akan melompat ke dalam air yang melebihi kepalanya. Jika seseorang yang bukan perenang memandang lurus ke dalam air yang kedalamannya 2,00 m. Seberapa dalamkah air itu terlihat?
Jawab:
Situasinya yang diperlihatkan dalam gambar 4. Misalkan ada sebuah lingkaran P yang di cat di dasar kolam itu pada kedalam s = 2,00 m. Permukaan dan dibiaskan membentuk bayangan P’, karena M = 1 untuk sebuah permukaan datar maka bayangan itu sama besarnya dengan lingkaran aslinya, tetapi kedalaman s’ dari bayangan itu berbeda dengan kedalaman dari P tersebut. Untuk mencari s’, kita menggunakan,
na/s + nb/s’ = 0
(1,33/2,00 m) + (1,00/s’) = 0
s’ = –1,50 m
kedalaman semua itu kira-kira hanya tiga perempat dari kedalaman yang sebenarnya. Tanda negatif memperlihatkan bahwa bayangan itu maya dan berada pada sisi datangnya sinar dari permukaan yang dibiaskan.
Soal 4
Suatu akuarium berbentuk bola dengan jejari 60 cm berisi air yang indeks biasnya na = 4/3. Seekor ikan yang berada pada jarak 40 cm terhadap dinding akuarium sedang diamati oleh seseorang yang berjarak 90 cm dari dinding akuarium tersebut. Tentukan jarak orang ke ikan, (a) menurut orang dan (b) menurut ikan.
Jawab;
(a) orang melihat ikan
Bayangan ikan terjadi karena sinar datang dari ikan menuju mata orang. Dengan demikian, data dari soal ditulis sebagai berikut,
n1 = nair = 4/3 (sinar datang berada di air)
R = –60 cm (sinar mengenai permukaan cekung)
s = 4 cm (jarak ikan ke dinding akuarium)
untuk menentukan bayangan ikan kita menggunakan persamaan
n1/s + n2/s’ = (n2 – n1)/R
[(4/3)/40 cm] + 1/s’ = [1 – 4/3]/[–60 cm]
1/30 + 1/s’ = 1/180
1/s’ = –5/180
s’ = –36 cm
bayangan ikan bersifat maya karena s’ bertanda negatif. Jarak orang ke ikan menurut orang adalah 90 cm + 36 cm = 126 cm
(b) ikan melihat orang
R = 60 cm (sinar mengenai permukaan cembung)
s = 90 cm (jarak orang ke dinding akuarium)
untuk menentukan bayangan ikan kita menggunakan persamaan
n1/s + n2/s’ = (n2 – n1)/R
1/90 cm + (4/3)/s’ = [4/3 – 1]/[60 cm]
1/90 + 4/3s’ = 1/180
4/3s’ = –1/180
s’ = –240 cm
bayangan orang bersifat maya karena s’ bertanda negatif. Jarak orang ke orang ke ikan menurut ikan adalah 90 cm + 240 cm = 280 cm
Sebuah batang gelas berbentuk silinder dalam udara (Gambar 1) mempunyai indek bias 1,52. Satu ujung gerinda (digosok) menjadi berbentuk setengah bola dengan jari-jari R = 2,00 cm, (a) Carilah jarak bayangan dari sebuah benda kecil pada sumbu batang itu, 8,00 cm di sebelah kiri dari verteks. (b) Carilah perbesaran lateral dan (c) bagaimana jika batang gelas dicelupkan dalam air yang memiliki indeks bias 1,33 tentukan jarak bayangan dan pembesaran lateralnya!
Jawab:
Kita beri na = 1,00 (udara), nb = 1,52, R = +2,00 cm, dan s = +8,00 cm
(a) dengan menggunakan
na/s + nb/s’ = (nb – nb)/R
kita peroleh
(1,00/8,00 cm) + (1,52/s’) = (1,52 – 1,00)/+2,00 cm
s' = +11,3 cm
karena s’ positif, ini berarti bayangan itu terbentuk 11,3 cm di sebelah kanan dari verteks
 |
| Gambar 1: Gelas di udara |
(b) dengan menggunakan
M = –nas’/nbs
Kita peroleh
M = –(1,00 x 11,3 cm)/(1,52 x 8,00 cm) = –0,929
Bayangan menjadi agak lebih kecil dari benda tersebut, dan bayangan terbalik. Jika benda tersebut adalah sebuah panah yang tingginya 1,000 mm yang menunjuk ke atas, maka bayangannya adalah sebuah panah yang tingginya 0,929 mm, menunjuk ke bawah.
(c) Jika batang gelas dicelupkan dalam air, gambar bayangannya seperti gambar 2.
 | |
|
Dengan jarak bayangannya adalah
na/s + nb/s’ = (nb – nb)/R
(1,33/8,00 cm) + (1,52/s’) = (1,52 – 1,33)/+2,00 cm
s' = –21,3 cm
nilai negatif dari s’ berti bahwa setelah sinar-sinar itu dibiaskan oleh permukaan tersebut, sinar-sinar itu tidak mengumpul tetapi terlihat terpencar dari sebuah titik 21,3 cm di sebelah kiri verteks tersebut, (membentuk sebuah bayangan maya 21,3 cm)
pembesaran lateralnya adalah
M = –(1,33 x –21,3 cm)/(1,52 x 8,00 cm) = +2,33
Dalam kasus ini bayangan itu tegak (karena M positif) dan 2,33 kali besarnya benda itu.
Soal 2
Satu koin tertanam dalam bola kertas plastik bulat memiliki radius 3,0 cm. Indeks pembiasandari plastik adalah na = 1,50. Koin berada 2,0 cm dari tepi bola (Gambar 3). Tentukan posisi bayangan koin.
 |
| Gambar 3; Koin dalam bola plastik |
Sketsa jalannya sinar ditunjukkan pada gambar 3. Dengan menggunakan
na/s + nb/s’ = (nb – nb)/R
kita peroleh
(1,50/2,0 cm) + (1,00/s’) = (1,00 – 1,5)/–3,0 cm
s' = –1,7 cm
Soal 3
Pemilik kolam renang mengetahui bahwa kolam selalu terlihat lebih dangkal daripada kedalaman sebenarnya dan penting untuk mengidentifikasi bagian-bagian yang dalam secara menyolok sehingga orang yang tak dapat berenang tidak akan melompat ke dalam air yang melebihi kepalanya. Jika seseorang yang bukan perenang memandang lurus ke dalam air yang kedalamannya 2,00 m. Seberapa dalamkah air itu terlihat?
 |
| Gambar 4: Seorang anak sedang berada di tepi sebuah kolam dan melihat kedalaman kolam seolah-olah dangkal |
Situasinya yang diperlihatkan dalam gambar 4. Misalkan ada sebuah lingkaran P yang di cat di dasar kolam itu pada kedalam s = 2,00 m. Permukaan dan dibiaskan membentuk bayangan P’, karena M = 1 untuk sebuah permukaan datar maka bayangan itu sama besarnya dengan lingkaran aslinya, tetapi kedalaman s’ dari bayangan itu berbeda dengan kedalaman dari P tersebut. Untuk mencari s’, kita menggunakan,
na/s + nb/s’ = 0
(1,33/2,00 m) + (1,00/s’) = 0
s’ = –1,50 m
kedalaman semua itu kira-kira hanya tiga perempat dari kedalaman yang sebenarnya. Tanda negatif memperlihatkan bahwa bayangan itu maya dan berada pada sisi datangnya sinar dari permukaan yang dibiaskan.
Soal 4
Suatu akuarium berbentuk bola dengan jejari 60 cm berisi air yang indeks biasnya na = 4/3. Seekor ikan yang berada pada jarak 40 cm terhadap dinding akuarium sedang diamati oleh seseorang yang berjarak 90 cm dari dinding akuarium tersebut. Tentukan jarak orang ke ikan, (a) menurut orang dan (b) menurut ikan.
Jawab;
(a) orang melihat ikan
 |
| Gambar 5 |
n1 = nair = 4/3 (sinar datang berada di air)
R = –60 cm (sinar mengenai permukaan cekung)
s = 4 cm (jarak ikan ke dinding akuarium)
untuk menentukan bayangan ikan kita menggunakan persamaan
n1/s + n2/s’ = (n2 – n1)/R
[(4/3)/40 cm] + 1/s’ = [1 – 4/3]/[–60 cm]
1/30 + 1/s’ = 1/180
1/s’ = –5/180
s’ = –36 cm
bayangan ikan bersifat maya karena s’ bertanda negatif. Jarak orang ke ikan menurut orang adalah 90 cm + 36 cm = 126 cm
(b) ikan melihat orang
 |
| Gambar 6 |
Bayangan orang tampak oleh ikan karena sinar datang dari orang ke mata ikan. Dengan demikian,
n1 = nudara = 1 (sinar datang berada di udara)R = 60 cm (sinar mengenai permukaan cembung)
s = 90 cm (jarak orang ke dinding akuarium)
untuk menentukan bayangan ikan kita menggunakan persamaan
n1/s + n2/s’ = (n2 – n1)/R
1/90 cm + (4/3)/s’ = [4/3 – 1]/[60 cm]
1/90 + 4/3s’ = 1/180
4/3s’ = –1/180
s’ = –240 cm
bayangan orang bersifat maya karena s’ bertanda negatif. Jarak orang ke orang ke ikan menurut ikan adalah 90 cm + 240 cm = 280 cm
Post a Comment for "soal dan penyelesaian pembiasan pada bidang lengkung"
Sobat Fisika! Berikan Komentar di kolom komentar dengan bahasa yang sopan dan sesuai isi konten...Terimasih untuk kunjunganmu di blog ini, semoga bermanfaat!