Soal Hukum Newton dan Pembahasannya 8

Soal 1
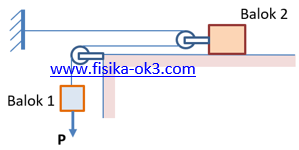
Perhatikan gambar. Balok 2 (massa 2 kg) pada permukaan horizontal dihubungkan ke balok 1 (massa 1 kg) melalui seutas tali dan dua katrol licin. Koefisien gesekan statis dan kinetis antara balok 2 dan permukaan masing-masing adalah 0,60 dan 0,40. Suatu gaya dengan besar P dikerjakan secara langsung pada balok 1.

(a) Berapa nilai terkecil P yang akan menyebabkan balok bergerak? Suatu nilai P yang lebih besar dikerjakan untuk membuat balok bergerak dan kemudian gaya P ini dihilangkan.
(b) Jika balok 2 bergerak dengan jarak d dalam selang waktu tertentu t, berapa jauh balok 1 telah bergerak?
(c) Bagaimana hubungan antara percepatan a₁dari balok 1 dan percepatan a₂ dari balok 2?
(d) Berapa nilai-nilai a₁ dan a₂ tersebut?

Jawab:
Diketahui: µ_s = 0,6, µ_k = 0,4, w₁ = 10 N dan w₂ = 20 N,

(a)

Gaya gesek statis, f_s,maks = µ_sw₂ = 0,6(20 N) = 12 N, dan

Gaya gesek kinetis, f_k = µ_kw₂ = 0,4(20 N) = 8 N,

Dari data, w₁ < f_s,maks (balok masih diam)

Maka gaya total gaya yang menyebabkan balok bergerak minimal sama dengan gaya gesek statis maksimum,

P + 10 N = f_s,maks

P_min = 12 N – 10 N = 2 N

(b)

x₂ = posisi balok 2 dari dinding, x₁ = posisi balok 1 dari dinding dan l = posisi balok 2 dari katrol K₁. Dari gambar di atas kita peroleh:

x₂ = x₁ + l

Panjang tali yang sedikit melilit katrol dapat kita abaikan.

Total panjang tali (dari dinding ke katrol K₁) adalah L = x₂ + l dan tidak berubah seiring waktu. Maka l = L – x₂, sehingga

x₂ = x₁ + (L – x₂) = x₁ – L – x₂

2x₂ = x₁ – L

atau
2d = x­₁ – L = pergeseran balok 1

(c) dari bagian (b) L adalah konstanta (nilainya tetap), maka kita peroleh

2d²x₂/dt² = d²x₁/dt²

Tetapi sisi kiri persamaan ini adalah percepatan balok 2 dan sisi kanan adalah percepatan balok 1, atau percepatan balok 1 adalah dua kali lipat dari percepatan balok 2:

a₁ = 2a₂

(d) (untuk kasus ini sistem telah bergerak atau P sudah tidak bekerja) tinjau balok 2, menurut hukum II Newton,

2T – f_k = m₂a₂

2T – 8 N = 2a₂ = a₁                  (*)

Tinjaun balok 1:

10 N – T = m₁a₁

10 N – T = a₁ atau

20 N – 2T = 2a₁   (**)

Maka jumlahkan persamaan (*) dan (**), kita peroleh

12 N = 3a₁

a₁ = 4 m/s² dan a₂ = ½a₁ = 2 m/s².

Soal 2
Sebuah truk bak terbuka membawa sebuah peti. Peti tidak diikat terhadap lantai tetapi koefisien gesek statis antara peti dan papan truk adalah 0,70. Ketika lampu merah berganti hijau pada suatu jalan raya datar, supir mulai mempercepat truknya, berapakah percepatan maksimum truk agar peti tidak meluncur ke belakang terhadap lantai truk? jika peti berada 3 meter dari ujung bak terbuka, akankah peti itu jatuh dari truk dalam 2,0 sekon pertama dari geraknya ketika supir tepat melampaui percepatan maksimum ini? ambil koefisien gerakan kinetis µ_k = 0,6.

Jawab:
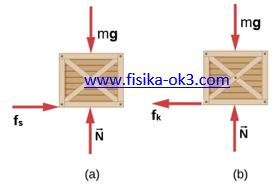
Gaya gesek statis antara peti dan lantai truk, f_s,p = µ_smg. Gaya horisontal yang mempercepat peti terhadap tanah hanya gaya tunggal f_s,p sehingga menggunakan hukum II Newton pada peti arah horisontal kita peroleh

∑F_peti = ma_peti,tanah

f_s,p = ma_peti,tanah

µ_smg = ma_peti,tanah

nilai a_truk,tanah = a_peti,tanah = a, maka

a_maks = µ_sg = 0,70(10 m/s²) = 7,0 m/s²

Jika percepatan truk a > a_maks, maka peti akan bergerak berlawanan dengan arah gerak truk akibat adanya gaya gesek kinetis, maka percepatan peti adalah

∑F_peti = ma_peti,truk

f_k = ma_peti,truk

µ_kmg = ma_peti,truk

a_peti,truk = µ_kg = 0,6 x 10 m/s² = 6 m/s²

dan peti akan bergeser sejauh (dari keadaan diam)

Δx = v₀t + ½ at² = 0 + ½ (6 m/s²)(2,0 s)²

Δx = 12,0 m, artinya peti akan jatuh dari truk