Soal dan penyelesaian gaya lorentz

Soal  1
Dua kawat panjang sejajar X dan Y masing-masing membawa arus 10 A dan terpisah sejauh 5 cm, seperti gambar di samping. Tentukan besar gaya per meter yang dikerjakan pada kawat.
  

Jawab;
Kedua kawat dialiri arus yang sama besar i₁ = i₂ = i = 10 A; jarak pisah a = 5 cm = 0,05 m, maka besar gaya per meter yang dikerjakan pada kedua kawat adalah
F/L = μ₀i²/(2πa)
F/L = [4π x 10^-7 x 10²]/(2π x 0,05)
      = 4,0 x 10^-6 N/m

Soal  2
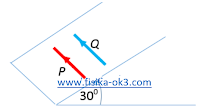
Dalam gambar di samping, dua kawat sejajar P dan Q, panjang sama 0,1 m masing-masing membawa arus 10 A. Jarak antara kedua kawat 0,05 m dan Q tetap diam karena adanya gaya magnetik yang dikerjakan P pada Q. Jika sudut antara bidang dengan arah mendatar 30⁰, tentukan berat kawat Q.

Jawab;
Perhatikan titik A pada gambar di atas θ + 30⁰ = 90⁰ maka θ = 60⁰.
Perhatikan titik B, gaya-gaya yang bekerja pada kawat Q di titik B adalah gaya tolak kawat berarus P pada kawat Q (diberi nama F) dan gaya berat w.
Gaya tolak tolak kawat P dan Q dihitung dengan persamaan,
F/L = μ₀i²/(2πa)
F = μ₀i²L/(2πa)
Komponen gaya F pada arah w, diberi nama F_w adalah
Cos θ = F/F_w
F_W = F/cos θ
F_W = μ₀i²L/(2πa cos θ)

Supaya kawat Q diam, maka berat kawat Q, yaitu w, harus seimbang dengan F_w, sehingga dapat kita tuliskan
w = F_w = μ₀i²L/(2πa cos θ)
karena i = 10 A, L = 0,1 m, jarak pisah a = 0,05 m, maka
w = [4π x 10^-7 x 10² x 0,1]/(2π x 0,05 cos 60⁰)
w = 8,0 x 10^-5 N

Soal  3
Gambar di bawah ini menunjukkan suatu kawat lurus sangat panjang yang membawa arus 5A. Kawat ini berada 2 cm dari sisi terdekat AD dari kumparan segiempat ABCD, yang membawa arus 2 A dan digantung vertikal di titik tengah AB. Jika ABCD memiliki ukuran 6 cm x 3 cm seperti yang ditunjukkan, hitung resultan gaya pada kumparan dan nyatakan pengaruhnya pada kumparan.

Jawab;
Gaya-gaya pada sisi AB dan sisi CD akibat medan magnet yang ditimbulkan oleh kawat berarus i₁, besarnya sama dan arahnya berlawanan, sehingga resultannya sama dengan nol. Gaya-gaya pada sisi DA dan BC yang disebabkan oleh kawat berarus i₁ dapat ditentukan arahnya sebagai berikut. Sisi kawat AD dan kawat berarus i₁ dialiri arus yang berlawanan arah, sehingga sisi AD akan ditolak oleh kawat i₁ dengan gaya F_AD ke kanan seperti yang ditunjukkan pada gambar. Sisi kawat BC dan kawat berarus i₁ dialiri arus yang searah, sehingga sisi BC akan ditarik oleh kawat i₁ dengan gaya F_BC ke kiri seperti di gambar.

Besar gaya F_AD dan F_BC dihitung dengan
F_AD/AD = μ₀i₁i₂/(2πa₁) maka F_AD = μ₀i₁i₂L/(2πa₁) dan
F_BC/BC = μ₀i₁i₂/(2πa₂) maka F_BC = μ₀i₁i₂L/(2πa₂)
Dengan AD = BC = L,
Karena a₁ < a₂, maka F_AD > F_BC dan karena keduanya berlawanan arah, maka resultan gaya pada kumparan adalah
F_ABCD = F_AD – F_BC searah F_AD yaitu ke kanan
F_ABCD = [μ₀i₁i₂L/2π][(a₂ – a₁)/a₁a₂]
Dengan kuat arua pada masing-masing kawat i₁ = 5 A dan i₂ = 2 A, L = 6 cm = 0,06 m, a₂ = 5 cm = 0,05 m, a₁ = 2 cm = 0,02 m, maka
F_ABCD = [4π x 10^-7 x 5 x 2 x 0,06/2π][(0,05 – 0,02)/0,05 x 0,02]
F_ABCD = 3,6 x 10^-6 N ke kanan